저는 면접을 하게 되면 전자회로를 공부하기 시작할 때 배우는 가장 기본적인 문제를 묻곤 합니다. 기본을 아는 사람은 공부하면서 스스로 그 영역을 넓혀갈 수 있거든요. 이것은 저를 면접했던 분께 배운 것이기도 합니다.
연결된 저항의 합성용량, 커패시턴스의 합성용량을 구하는 것도 그 기본적인 내용 중의 하나입니다. 이 문제는 심지어 고등학교 물리 시간에도 나오죠, 아마? 그런데, 의외로 이것과 관련된 대화에서 많이 당황합니다. 대화를 이어 나가다 보면 왜 그렇게 되었느냐는 질문에는 모두 말문이 막혀 버리는 경우가 많습니다. 단순히 공식을 외워서 답을 구하는 것만 관심을 두는 것이죠. 물론 그렇게 하면 답은 구할 수 있고, 시험에서 좋은 성적은 받을 수 있겠지만, 근본적인 문제를 이해하고 해결하는 데에는 부족할 수 있습니다.
근본적인 대답은 전류와 전압의 관계가 어떻게 변화했는가 하는 것입니다. 전자공학의 모든 문제가 이 전류와 전압의 관계이니까요.
저항(resistance)의 경우를 살펴보도록 하죠. 저항의 용량 합성이라고 하면, 병렬연결인 경우의 공식이니 직렬연결인 경우의 공식하고 따지는데, 그런 것 모두 제쳐 두겠습니다. 그래야 이것이 병렬연결인지 직렬연결인지 마구마구 헷갈릴 때에도 문제를 해결할 수 있을 테니까요.
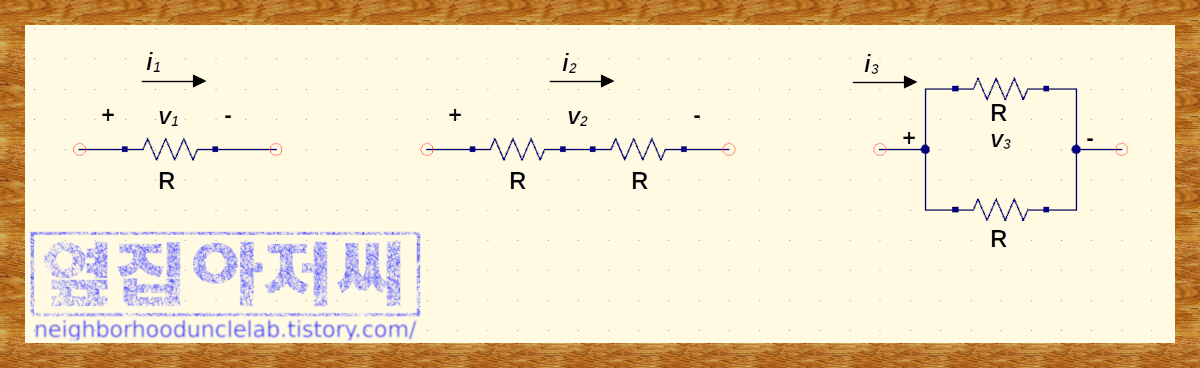
가장 왼쪽에 있는 그림에서 $i_1$과 $v_1$의 관계로부터 저항의 값 $$R=\frac{v_1}{i_1}$$으로 주어집니다. 옴 선생님의 옴의 법칙이지요. 전류와 전압의 관계로부터 저항을 알 수 있습니다.
가운데 있는 두 번째 그림에서는 두 저항에 흐르는 전류는 $i_2$로 동일합니다. 두 저항의 양쪽 끝에서 측정하는 전압 $v_2$는 각 저항의 전압의 합입니다. 이것은 키르히호프의 전압법칙(KVL)이지요. 첫번째와 마찬가지로 풀어볼 수 있겠지요.
$$R_{eq}=\frac{v_2}{i_2}\quad\quad\text{(1)}$$
$$v_2=i_2R+i_2R\quad\text{(2)}$$
(2)의 양변을 $i_2$로 나누면 $$\frac{v_2}{i_2}=R+R=2R=R_{eq}$$
이것으로부터 직렬연결된 저항의 합성용량은 모든 저항값을 더한다는 공식이 나온 것입니다.
가장 오른쪽의 세 번째 그림에서는 두 저항의 양쪽은 서로 연결되어 있고, 각 저항의 양쪽에 인가되는 전압은 $v_3$로 같습니다. 그래서 각 저항에 흐르는 전류는 $\frac{v_3}{R}$이 됩니다. 전체 전류 $i_3$는 각 저항에 흐르는 전류를 합친 것입니다. 이것은 키르히호프의 전류법칙(KCL)입니다.
$$R_{eq}=\frac{v_3}{i_3}\quad\quad\text{(3)}$$
$$i_3=\frac{v_3}{R}+\frac{v_3}{R}\quad\text(4)$$
(4)의 양변을 $v_3$로 나누면
$$\frac{i_3}{v_3}=\frac{1}{R_{eq}}=\frac{1}{R}+\frac{1}{R}\quad\text(5)$$
(5)의 역수를 취하여, $$R_{eq}=\frac{1}{{\frac{1}{R}}+{\frac{1}{R}}}=\frac{1}{\frac{2}{R}}=\frac{R}{2}$$
이것으로부터 병렬연결된 저항의 합성용량의 역수는 각 저항값의 역수의 합과 같다는 공식이 나온 것입니다.
커패시턴스(capacitance) 용량의 합성은 어떨까요? 커패시턴스(capacitance)의 경우에는 미분과 적분의 개념이 들어가니, 이 개념을 아직 적립하기 전이라면 어렵겠지만, 기본적인 접근은 동일합니다. 키르히호프의 법칙은 커패시턴스의 경우에도 적용이 됩니다.

저항의 경우와 똑같이 가장 왼쪽에 있는 그림에서부터 출발을 해 보겠습니다.
커패시터가 하나인 경우 - 흑은 이것이 하나로 합성된 용량이라고 하더라도 -, 전류와 전압의 관계는 $$i_1=C\frac{\text{d}v_1}{\text{d}t}$$로 주어집니다. 이것은 적분을 통하여 $$v_1=\frac{1}{C}\int{i_1}\text{d}t+V_0$$와 같이 쓸 수 있습니다. $V_0$는 초기 전압인데, 이것이 0인 경우에는 무시가 됩니다.
두 번째 그림에서는 두 커패시터에 흐르는 전류 $i_2$는 동일하고, 각 커패시터의 전압의 합이 $v_2$가 됩니다. 이것으로부터 $$v_2=\frac{1}{C}\int{i_2}\text{d}t+\frac{1}{C}\int{i_2}\text{d}t+V_0=(\frac{1}{C}+\frac{1}{C})\int{i_2}\text{d}t+V_0\quad(6)$$
(6)의 양변을 다시 미분하여 정리합니다.
$$i_2=\frac{1}{\frac{1}{C}+\frac{1}{C}}\frac{\text{d}v_2}{\text{d}t}\quad(7)$$
(7)로부터 $$C_{eq}=\frac{1}{\frac{1}{C}+\frac{1}{C}}=\frac{1}{\frac{2}{C}}=\frac{C}{2}$$가 됩니다.
이것이 직렬연결된 커패시터의 합성용량의 역수는 각 커패시턴스의 역수의 합과 같다는 공식이 나온 이유입니다. 미분적분을 왔다 갔다 하다 보니 좀 어렵게 보이지만 원리는 같습니다.
세 번째 그림에서는 두 커패시터의 양쪽 전압은 $v_3$로 같고, 전체 전류 $i_3$는 두 커패시터의 전류의 합과 같다에서 시작을 합니다. 각 커패시터의 전류는 $C\frac{\text{d}v_3}{\text{d}t}$가 되죠?
$$ i_3=C\frac{\text{d}v_3}{\text{d}t}+C\frac{\text{d}v_3}{\text{d}t}=(C+C)\frac{\text{d}v_3}{\text{d}t}\quad(8)$$
(8)로부터 $$C_{eq}=C+C=2C$$입니다.
이것으로 병렬연결된 두 커패시터의 합성용량은 두 커패시턴스의 합과 같다고 이야기되는 것입니다.
위에서 저항의 경우, 커패시터의 경우 모두 같은 용량의 저항 또는 커패시터를 2개 직렬, 병렬 연결하였습니다. 이와 같은 경우에는 합성용량이 2배 혹은 $\frac{1}{2}$가 되는 것입니다. 들여다보면 저항과 커패시턴스의 합성용량의 구하는 공식이 저항과 커패시터가 서로 반대인 것을 알 수 있습니다. 공식을 외우고 있다면 합성용량을 금방 구할 수도 있을 것입니다. 하지만, 중요한 것은 합성용량이라고 하는 것은 전체 전압과 전류에 어떤 영향을 주느냐로 결정이 되는 것입니다. 그러니까 공식을 외우지 않아도 그 말이 무엇을 의미하는지를 안다면 충분히 구할 수 있다는 것이지요.
대표적인 수동소자 중에는 저항(resistor), 커패시터(capacitor)와 함께 인덕터(inductor)라는 것이 있습니다. 인덕터의 전류와 전압의 관계는 $$v=L\frac{\text{d}i}{\text{d}t}$$로 나타냅니다. 인덕터의 합성용량 구하기도 스스로 한 번 해 보세요. 전압과 전류의 관계를 이용하는 것은 완전히 똑같습니다.
다시 말하지만, 기본을 아는 사람은 어떤 것이라도 배울 수 있습니다.
'전자공학을 즐겁게 > 전자공학 컴퓨터 잡지식' 카테고리의 다른 글
| FreeCAD 무작정 따라하기 - Part Design Workbench에서 모델링 하기 (0) | 2023.12.27 |
|---|---|
| Thunderbird 메일 클라이언트가 갑자기 @hotmail.com 계정의 메일을 보내지 못한다 - 2단계 인증과 앱 암호 (0) | 2023.09.06 |
| 전자회로의 청진기 멀티미터 (Multimeter) (0) | 2022.05.18 |
| 직류 전원 공급 장치 (DC Power Supply) (0) | 2022.04.20 |
| 납땜인두로 납땜하는 법 (Hand Soldering with Soldering Iron) (0) | 2022.04.13 |




