전지의 병렬연결, 그리고 전지의 지속 시간

이전 포스트에 전지의 병렬연결을 언급하지 않았습니다.이번 포스트에서 마저 살펴 보도록 하겠습니다.

 

전지 2개를 병렬로 연결하였습니다. 전구에 흐르는 전류는 전구 양쪽에 가해지는 전압과 전구의 저항에 의하여 이전과 같지만, 그 전류는 이제 2개의 전지로부터 나누어서 받게 됩니다. 오른쪽 그림에서 $I_5$와 $I_6$가 같다면 절반씩 받게 되는 셈이지요.

지난 포스트에서 전지의 병렬연결을 언급하지 않은 것은 이러한 구성에서 전구에 가해지는 전압과 흐르는 전류는 배터리를 1개 연결했을 때와 동일하기 때문입니다. 차이가 있다면 전구에 흐르는 전류는 키르히호프의 전류 법칙(KCL; Kirchhoff’s Current Law)에 의해서 전지 2개에서 나누어 공급하게 됩니다. 한 손으로 들던 물건을 두 손으로 들게 된 것입니다. 전지의 병렬 연결은 전지의 입장에서 살펴 보아야 합니다.

728x90

당연히 전지가 얼마나 지속될 수 있느냐에 대해서 살펴볼 텐데, 그냥 당연하게 여겨질 수 있습니다. 2개 전지가 나누어 공급을 했으니 당연히 2배의 시간동안 사용할 수 있겠지라고 직관적으로 답을 할 수 있을 것입니다. 그럼 그 2배의 시간은? 
설계한 회로가 주어진 에너지원으로 얼마나 오래 동작할 수 있느냐는 시스템 설계에서 중요한 부분을 차지하는 한 부분입니다. 엔지니어들은 설계한 시스템이 주어진 에너지로 가능한 한 오래 동작할 수 있도록 여러 가지 노력을 합니다.
전에 전지는 전하를 가득 담은 통과 같다고 말한 적이 있습니다. 전하의 양, 즉 전하량은 전류를 얼마나 오래 공급할 수 있는가에 대한 답이 됩니다. 물탱크에 가득 찬 물과 같다고 할까요. 에너지와 전하량이라는 말이 번갈아 쓰이고 있어서 혼란수러울 수도 있을 텐데, 에너지는 전하량과 비례하는 관계에 있다고 할 수 있기 때문에 전하량을 표시하는 것으로 대신할 수 있는 것입니다.

전하량은 전류와 시간에 비례합니다.

 

요즘은 어디에서라도 스마트 폰을 충전할 수 있도록 보조배터리를 많이 가지고 다니는데요, 이 보조배터리를 10000mAh짜리 배터리니 20000mAh 배터리니 하고 말하는 것을 볼 수 있습니다. 단순히 숫자로 보아도 20000이 10000보다 2배 크다고 느껴지지요? 단위를 자세히 뜯어 보도록 하겠습니다. 

1mAh는 1mA의 전류를 1시간(hour) 흘렸을 때의 전하량입니다. 1mAh는 3.6C와 같습니다.

 

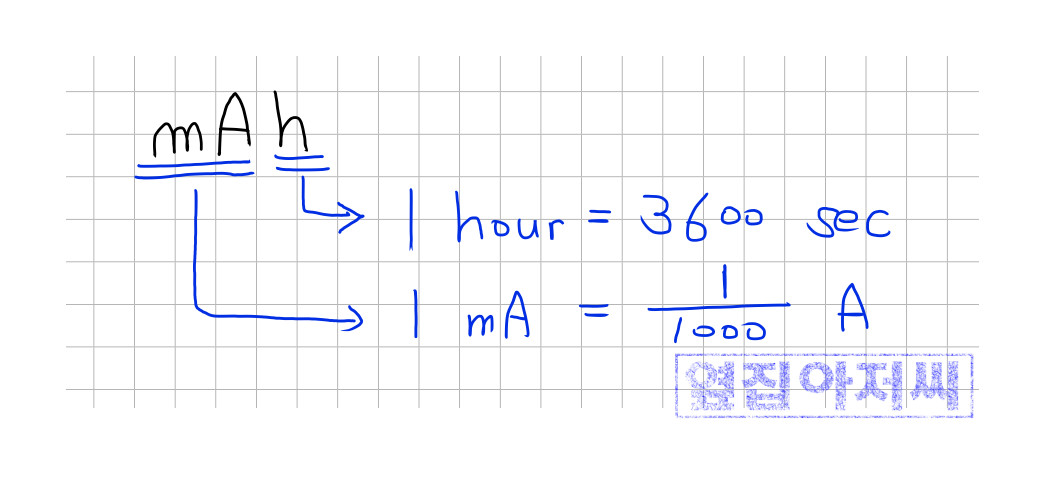
아하~ 1mAh라는 것은 1000분의 1 암페어[A]의 전류를 1시간 혹은 3600초 동안 흘릴 수 있는 전하량이라는 것이군요.

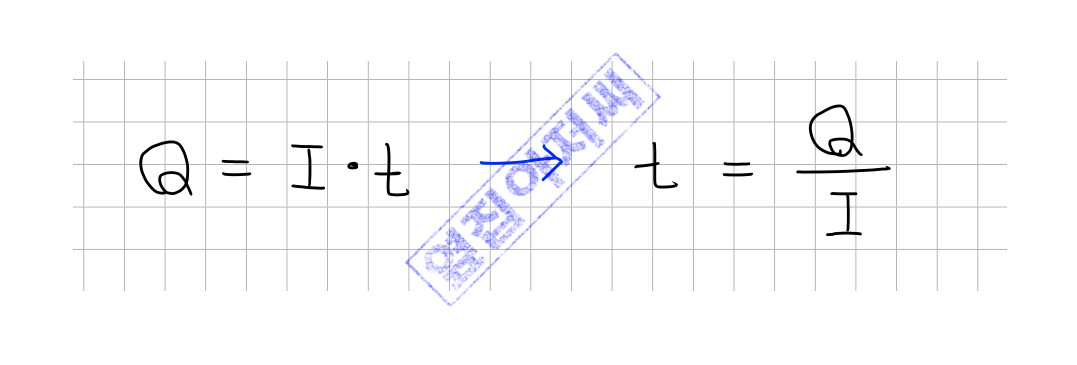
이 전하량이 모두 소모되면 전지는 모두 방전되었다고 합니다. 그 때까지의 시간을 전지의 지속 시간 (Battery Life Time)이라고 합니다. 예를 들면 나의 회로가 1000mA를 소모한다면 10000mAh 용량을 갖는 전지는 10시간이면 모두 방전될 것이다라고 예측을 해 볼 수 있습니다. 이 시간을 늘이고 싶다면? 전지의 용량을 늘이는 방법을 택하던가, 좀 더 고민을 해서 회로에서 소모하는 전류를 줄이는 노력을 하게 됩니다. 

대략적으로 전지의 지속시간을 아래 수식으로 예측하게 됩니다. 

전지의 지속시간(Battery Lifetime)은 전하량과 전류 관계를 이용하여 예측합니다.